Lorem ipsum dolor sit amet, consectetur adipiscing elit. Curabitur et congue nulla. Mauris at lobortis est, sed tincidunt massa. Nam massa elit, ultrices commodo iaculis non, mattis vel magna. Proin at justo bibendum, lacinia massa ut, ullamcorper leo. Vivamus malesuada ipsum vitae posuere pharetra. Quisque accumsan lorem vel neque ornare, sit amet aliquet augue facilisis. Donec vel odio ac ipsum mattis eleifend. Cras pulvinar, libero ac condimentum elementum, felis nisl eleifend odio, sit amet pulvinar ipsum risus vel risus. Sed porta tortor vel nulla commodo interdum. Curabitur id porta elit. Morbi et lobortis sapien, eget porta lectus. Sed non sem metus. Nulla sodales felis vitae metus porta efficitur. Cras aliquam ullamcorper eros, et tempor turpis sollicitudin non. Donec pretium nunc augue, at dignissim metus feugiat non. Suspendisse ac mi sit amet arcu bibendum pulvinar ac non lectus.

Vivamus sed nibh mi. Praesent et ex nec ante semper volutpat. Integer velit augue, pharetra ut egestas vel, maximus vitae felis. Nam hendrerit, libero in condimentum rhoncus, elit elit lobortis arcu, pharetra volutpat purus felis sed nisl. Vestibulum tincidunt facilisis mauris, et ultricies dui imperdiet a. Pellentesque feugiat elit sit amet justo sagittis, eget malesuada orci molestie. Sed sed nisl pulvinar, sodales enim laoreet, pretium risus. Aenean elementum a velit eget lacinia. Maecenas facilisis dolor ac nunc varius, et cursus magna vulputate. Sed facilisis risus magna, eget feugiat sapien mattis eu. Nulla cursus gravida erat. Nulla porta porttitor semper. Maecenas mauris urna, euismod eu libero vitae, porta fringilla quam. Ut ultrices sollicitudin gravida. Aliquam nulla elit, finibus ac tortor id, facilisis viverra lacus. Nullam ut justo at metus pharetra sodales ut ac sem.

Mauris pulvinar lacus urna, et convallis diam mollis vel. Fusce blandit, sem et porttitor dignissim, mi sem hendrerit augue, vitae ultricies mi urna vel enim. Sed imperdiet eget magna quis hendrerit. Aliquam vitae mi massa. Mauris dignissim tincidunt massa et dignissim. Ut a quam commodo, ornare massa tincidunt, feugiat libero. Vestibulum ante ipsum primis in faucibus orci luctus et ultrices posuere cubilia curae; Mauris sodales felis sit amet tellus rhoncus iaculis. Proin hendrerit neque et sapien sagittis, ac pellentesque sapien fringilla. Fusce elit dolor, fermentum a lorem sit amet, lacinia vestibulum sapien. Vivamus mattis nisi ut semper consectetur.

Cras vel elit eget erat posuere bibendum eget ac justo. Nunc a diam sed felis faucibus rutrum. Interdum et malesuada fames ac ante ipsum primis in faucibus. Nulla tincidunt massa in est porttitor, nec semper diam pharetra. Etiam finibus dignissim elit quis cursus. Ut euismod purus diam, sed lacinia nunc tincidunt vel. Ut congue lobortis ultrices. Sed nunc purus, volutpat non tellus et, lobortis auctor dolor. Vivamus varius dui neque, eu feugiat risus rutrum ultrices. Sed ligula augue, vestibulum nec imperdiet eu, condimentum eu nulla. Aenean vulputate eros erat, eget porttitor magna congue vitae. Aenean iaculis ligula eu vehicula semper. Vivamus non bibendum tellus. Donec sit amet nulla mollis, rutrum tellus vel, tristique enim.

Mauris suscipit eleifend odio non vehicula. Nam semper massa purus. Quisque nisi elit, egestas a elit feugiat, vestibulum porttitor sapien. Quisque interdum, sapien placerat eleifend vulputate, ex enim lacinia velit, quis blandit velit lectus id lorem. Pellentesque commodo sed ante quis fermentum. Pellentesque vestibulum nibh risus, id facilisis turpis faucibus eu. Sed eget faucibus turpis. Donec vulputate lacus eget erat tristique finibus.

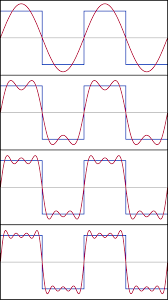
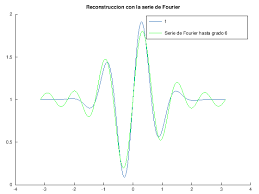
Una serie de Fourier es una serie infinita que converge puntualmente a una función periódica y continua. Puede ser solo a trozos de funciones (por partes), pero continua en esas partes. Las series de Fourier constituyen la herramienta matemática básica del análisis de Fourier empleado para analizar funciones periódicas a través de la descomposición de dicha función en una suma infinita de funciones sinusoidales mucho más simples (como combinación de senos y cosenos con frecuencias enteras). El nombre se debe al matemático francés Jean-Baptiste Joseph Fourier, que desarrolló la teoría cuando estudiaba la ecuación del calor. Fue el primero que estudió tales series sistemáticamente, y publicó sus resultados iniciales en 1807 y 1811. Esta área de investigación se llama algunas veces análisis armónico.